TEST WED

Reviewed the solutions to the provincial exam for January 2005. If you are looking for further review, the questions on exponentials and logarithms from June 2005 would be a good place to start; they are available on the sidebar. The blue study guide also contains some good info.

Logarithms and Word Problems

We will be concluding logarithms on Friday by correcting a few more word problems dealing with logarithms.

The key to tackling these questions is to change the words into an exponential function in the form y=ab^(x/n). A few points of advice:

• If you're getting caught up on the terminology, making a table of values is a very good strategy. Write down the first two or three terms, then use this information to find the equation y=ab^(x/n)
• be careful with levels of interest; remember that when something doesn't change the base is 1. So if you are gaining 8% interest the base will be (1+0.08) or (1.08). Similarly, if something is depreciating by 10% then the base will be (1-.10) or (0.9).
• Your base should NEVER be negative in the scope of these questions, so if you have a negative number as the base you messed up somewhere.
  

Solving a word problem which uses logarithms contains two distinct steps. First is deriving the exponential equations from the word problem as in the picture below.

From here you have two options: you can either work the problem out using the laws of logarithms (you have an unknown in the exponents and the bases cannot be made equal, so use logarithms). Please use more significant figures than I did -_- (4 would be sufficient)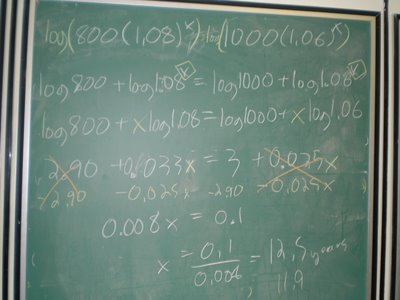

Or you can graph the intersection points between the two graphs. If you choose to do this, the board below shows how much work would be required on the provincial exam (you have to play with your window settings a bit on the calculator to get a nice picture)

Homework is the Multiple Choice questions from the January 2005 Provincial exam handed out in class, (10-18).

Laws of Logarithms

Sorry for the delay, here are some class notes from Tuesday. I misplaced my camera so no pictures from today.

Homework was continuing work on simplifying the logarithms from the sheet handed out in class.

Rewriting exponents as logarithms

Some of the problems we worked out in class dealing with logarithms. Homework is p.175 #15 and p.203 #33,34,35.

Exponential Word Problems and Logarithms

I will put more detail here on Saturday, but the homework was as follows:

p.174 #13, 12, 14 (in that order)

This is VERY important to have done, even if you weren't here, so I'll be posting notes online for those who missed class on Saturday. We're talking "I'm calling home for those who weren't here" important.

Table of Values -> Exponential Equation

Today we derived transferring from a table of values of a geometric sequence (ie. exponential) to an exponential function of the form:

y = ab^(x/n)

Where:

a = the value of y when x=0
b = the common ratio between subsequent terms (divide present term by previous term)
n = the change in the values of x

Homework:

p.136#30, p.135 #26 (equation only)

Graphing y=ab^x + c

Double period. We investigated the following 8 exponential functions using the TI-83. If you MISSED the class, you should be certain to do each of these:

y = 2^x
y+4 = 3(2)^x
y-3 = 2^x
y+1 = 0.5(2)^x
y = 16(2)^x
y = 4(2)^(x+2)
y = 2^(x+4)
y-3 = 0.5^(x-3)

For each of these functions, we found:

• Growth or decay (growth when the base > 1, decay when 0 <>
• y-intercept (set x=0)
• root (using the graphing calculator to calculate, if it exists)
• equation of the asymptote (equal to the vertical translation, OR graph the function in the TI-83, look at your table of values, and see what value y is approaching as x gets larger or smaller)

After investigating these questions, the following was assigned for homework:

p.148#6,p.149#8(B,C)

for each of these questions, find ONLY:

• Growth or decay?
• y-intercept
• equation of the asymptote
• Root (if it exists)
• Domain/Range

Plus find the domain and range for each of the previous 8 equations.

Law of Exponentials + Graphing y=ab^x

We corrected homework assignments from the previous classes as well as completing p.169 #22 s-x.

Homework: Draw a quick sketch of the the functions below and list the asymptote and y-intercept of each:

y=3(0.7)^x
y=(0.7)^x
y=0.5(0.7)^x
y=3(1.5)^x
y=(1.5)^x
y=0.5(1.5)^x

in addition p.129#9,10

Test returned

Test #2 was returned today, marked out of 34. Class average was a 22.4. Corrections for this test, written out in detail on a separate sheet of paper and stapled to the front of the test, will be due on Friday as an assignment.

Quiz day + solving for an unkown in the expoonential.

The bulk of this period was used to write a quiz on exponentials.

In addition, we checked solutions from Friday's work. Homework for tonight:

p.165 #12a,b,e,g,h (for those who did not finish Friday's homework)
p.203 #26

QUIZ MONDAY - Solving for an unknown in the exponent

A double dose of mathematics today! First period was more difficult questions concerning solving for the equation in the unknown. We worked on p.160 #14,16 in class.

Second period involved correcting the work from the previous period and rewriting radicals in terms of a base to an exponent. Homework for the weekend:

p.164 #7(odd only),8(odd only),10(odd only),12

The quiz on Monday will cover the following topics:

• Is an exponential function growth or decay? (discussed on p.114)
  
• Using the Laws of Exponents to simplify expressions (p.169 #22 a-p)
• Simplifying equations with negative/zero exponents (p.121 #38)
• Solving for an unknown in the exponent (p.160 #12,13,16)

I can point people in the direction of further example questions on request.

Solving for an unknown in the exponent

(Message board is coming soon)

We continued with simplifying using the laws of exponents, and began problems with the exponent in the unknown, such as:

25^x = 125^(x+1)

First try to reduce the bases to the smallest possible number (integer):

(5^2)^x = (5^3)^(x+1)

Simplify using the laws of exponents

5^2x = 5^(3x+3)

Now, since the bases are the same, the exponents must be the same as well. So,

2x = 3x + 3
-3x -3x
-x = -3
x = 3

Homework is p.160 #12,13

Laws of Exponents

Investigated the laws of exponents today (p.167) and simplifying expressions with common bases.

Homework: p.169 #22(A-P)